In Armageddon, a NASA guy comments that a plan to shoot a laser at the asteroid is like “shooting a b.b. gun at a freight train.” What would it take to stop an out-of-control freight train using only b.b. guns?
—Charles James O'Keefe
First of all, for the record, shooting asteroids with lasers is a great way to deflect them. Stopping a train with a BB gun might be harder.
A Red Ryder spring-piston lever-action air rifle fires a standard 0.177-caliber 0.33g steel BB at a muzzle velocity of 100 meters per second.
The GE Genesis Series I locomotive weighs 12 metric tons and travels at around 45 meters per second.
If you bounce a single BB off the front of the locomotive from point blank range, you slow it down by about a foot per day.

At one shot per second, it’d take over two days and nearly 200,000 BBs to bring the train to a halt—and by that point it would’ve stopped on its own anyway. (Based on the formulas on this page for the drag forces on a train, a back-of-the-envelope differential equation for the locomotive's motion suggests that on a flat track with no brakes, it would slow down on its own from 100 to 20 mph in ten or fifteen minutes).
Clearly, the Red Ryder isn’t cutting it.
It’s time to wade into the terrifying world of hardcore air rifle enthusiasts.
The Tactical Edition Drozd Blackbird is a high-end BB machine gun (of course there are BB machine guns). It fires 1200 rounds a minute at a muzzle velocity of over 200 meters per second. At those speeds, standard BBs are capable of fracturing bone.
Unfortunately, even instantaneously emptying the full 600 rounds into the front of the train would only reduce its speed by a small fraction of a percent.
A single person with a BB gun can't do it. But what if we had an army?

We’ll give each person a patch of ground two feet by four feet. This is a little cramped, but it should give them room to fire in an arc over the shoulder of the person in front of them. If we restrict them to 45 degrees in front of the train on either side of the track, we can pack about 100 people within 10 meters, 300 more within 20 meters, 550 more within 30 meters, and another 750 within 40 meters.
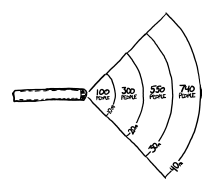
Most of the shooters are able to hit the train fairly straight-on. Integrating the momentum from all the different shooting angles shows that the fanned-out arrangement exerts on the train over 90% of the force that an ideal arrangement (with every gun directly in front of the train) would.
BBs experience a lot of drag, so the shots from those further away will reach the train at a lower speed. This page gives estimates for the drag forces on a BB at various speeds. I love the internet.
With all that in mind, let’s look at what happens when a crowd of people with BB machine guns try to stop a train. In fact, people have two arms, so let’s have them all dual-wield.
At t=0, the people within 50 meters of the train—all 2,500 of them—pull the triggers, unleashing 100,000 BBs per second. As the train plows ahead, people in front magically fly sideways off the tracks. This is unrealistic, but we can’t let them slow down the train with their bodies—that would be cheating.
As those people stop firing, people further down the tracks come into range and start shooting. The train is moving so quickly that any one person only gets off a few dozen rounds before the target moves past (or through) them.
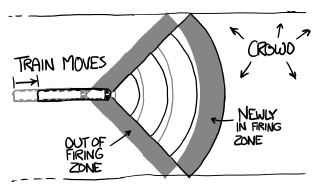
At any given time, there are 45,000 BBs in the air. But there’s a problem: When the steel balls bounce off the front of the train, they don’t disappear. They fly back at the shooters (who’ll probably shoot their eyes out) and into the line of fire. At its peak, this cloud of ricochets deflects nearly 1% of incoming shots via BB-BB collisions. This is a neat effect, but it doesn’t substantially interfere with our operation.
Unfortunately, even this hail of steel takes several excruciating minutes—and almost two kilometers of track—to stop the train. That means we’d need over 100,000 shooters lined up along the track, and arming them would cost in the neighborhood of $50 million.
We can do better, but we’ll have to relax the BB gun requirement.
The AK-47 has a muzzle velocity of 715 meters per second and fires a bullet which outweighs a steel BB by a factor of 25. The bullets go so fast that they penetrate into the body of the train (which means they’re a little less efficient at transferring momentum, but it doesn’t really matter).
Calculations show a crowd of 2,500 people firing two AK-47s each would be able to stop our runaway locomotive within the space of 30 meters—in only a second and a half. Mission accomplished.

... well.
The greatly reduced drag coefficient of machine gun ammo compared to steel ball bearings means we can shoot from a much greater distance. Let’s make the crowd 200 meters deep instead of 50.
At t=0, 40,000 people open fire. The AK-47 typically has a 30-round magazine and fires 10 shots per second. Within a third of a second, a quarter of a million bullets are in the air. Stray shots no doubt cause a lot of fatalities in the front of the crowd, but with a trained and disciplined group of shooters, the bulk of the shots could actually manage to hit the target.
At t=15 ms, the locomotive has inched forward by half a meter and encounters the leading edge of the bullet cloud.
By t=30 ms, the locomotive is being hit by a half dozen new bullets every millisecond.
At t=150 ms, the locomotive has crawled forward about six meters, but it’s absorbing several hundred bullets each millisecond. This has begun to slow its forward momentum (and tear it apart—let’s assume it’s loaded full of some kind of lightweight material that distributes the shock of the bullet evenly).
At around t=300ms, the full quarter of a million bullets are in the air. Most people have gotten off a total of six shots between their two guns. Interestingly, the bullets from the front rows of shooters occasionally catch up with—and collide with—slower bullets from the shooters behind them. This doesn’t happen a lot, but it does happen.
The locomotive creeps forward to seven meters, seven and a half, seven and three quarters … and then seven and a half again.
Success.
But the shooters have only fired about a dozen rounds so far. Their magazines are still mostly full.
At t=1s, almost a million shots have been fired. The locomotive is sliding backward at about 100 m/s (220 mph). At t=2s, the locomotive’s backward acceleration slows down quite a bit. This is partly because it’s starting to get out of range of the shooters. But it’s also because the locomotive is traveling at nearly the speed of sound, and the bullets are having a harder and harder time catching up. When they do, they have so little relative velocity that they can’t accelerate it much more.
By this point, drag from the atmosphere is the dominant force on the locomotive’s motion. The rear end lifts from the tracks, the locomotive starts to tumble, and finally disintegrates into a cloud of shrapnel and spent bullets.
Now bring on that asteroid.