Every now and then we have to insert a leap second because the Earth’s rotation is slowing down. Could we speed up Earth’s rotation, so that we do not need Leap Seconds?
—Anton (Berlin, Germany)
The Earth’s spin is slowing down. This is annoying.
One reason that it’s annoying is that it makes time standards more difficult. We already have way too many time standards, including:
- TAI, time based on an atomic clock, which ignores all motion of the Earth
- UT0 and UT1, time based on precise measurement of the Earth’s rotation
- GPS, the time standard used by GPS satellites
- UTC, the standard used in computing, which is like TAI but with leap seconds to keep it in sync with Earth
- TDT, TBT, TCB, and TCG, which are all even worse
This leads to all kinds of little headaches, particularly for programmers. For example, the clock in your smartphone’s GPS is 16 seconds out of sync with the phone’s system clock. This is because the system clock uses Coordinated Universal Time (which has leap seconds), but GPS time doesn’t. They were in sync in January of 1980 and probably never will be again.
Half a billion years ago (when the Earth was 4 billion years old, instead of 4.5), each day was 22 hours long instead of 24. The day has gotten longer because of tidal forces from the Moon.
Loosely speaking, here’s how tidal drag works: The Moon’s tides raise bulges in the Earth, but the Earth’s rotation moves those bulges out of line with the Moon. The Moon’s gravity tries to tug the bulges back into line, which exerts a twisting force on the Earth, slowing it down:

Strangely, the Earth is actually not slowing down as much as you’d expect from tidal drag. The biggest reason for the discrepancy is that during the last ice age, the continents were pushed down by the weight of the glaciers, and they’re still springing back into place. This has the effect of shifting mass toward the poles, closer to the axis of rotation:
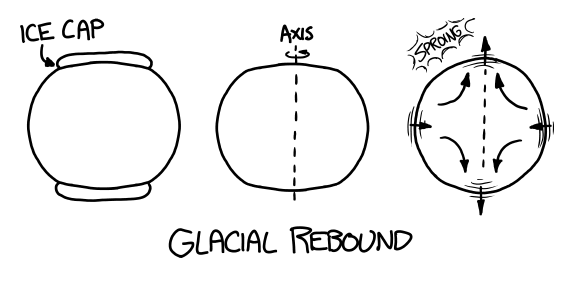
This makes us spin faster—or, at least, keeps us from slowing down as quickly.
At the moment, each day is about 0.8 milliseconds longer than the 86,400 seconds it needs to be to avoid adding leap seconds.
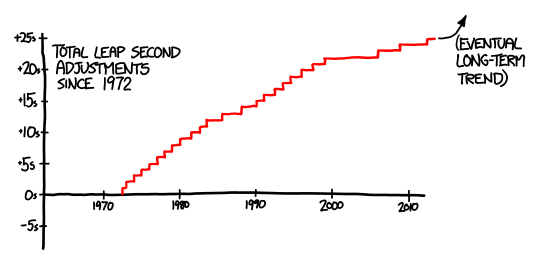
This difference fluctuates over time based on weather and other effects (it’s actually shortened a bit since the early 1990s), although in the long run, it will definitely get larger as the Earth slows.
If we wanted to get rid of leap seconds, we’d need to keep the Earth spinning at a more constant rate. This means speeding up the Earth and shortening each day by about 0.8 milliseconds.
This is a tough problem. Here are a few things that won’t work:
Spinning counterclockwise in a chair. It temporarily alters the Earth’s rate of rotation, but not enough to matter.
Putting rocket engines on the Equator. This won’t work because the exhaust would go into the atmosphere, which transmits the force back to the ground as wind drag—it’d be like making a bike go forward by pushing on the handlebars. If the engines were somehow mounted above the atmosphere, they’d be able to slow the Earth, but not by enough to accomplish our goal.
Triggering big earthquakes. This can alter the length of the day, but even those aren’t big enough to make a difference.
In the end, there’s only one solution: Hitting the Earth with asteroids.
Given enough time, we could send a spaceship (captained by an anti-Bruce Willis) to perform repeated flybys of a comet. Over time, the gravitational perturbation could steer the comet into a collision course with Earth. By hitting the Earth at the right angle, we would give it a push:

Even if the comet burns up in the atmosphere, its momentum is transmitted to the surface by wind drag (taking a matter of days). It takes about a decade for the core to sync up with the crust, so we’d have to plan the impact schedule carefully to avoid overshooting.
Here’s the bad news: To get enough spin, we have to hit the Earth with on the order of a billion liters of rock per second (several times the volumetric discharge rate of the Amazon). This adds up to about one six-mile dinosaur-killing asteroid every couple days. Humanity—and life—wouldn’t survive the bombardment long.
What about a steady stream of smaller asteroids?
If asteroid B-612 in The Little Prince is four meters across and made of rock, we’d need an average of around fifty thousand of them to enter the atmosphere each second to keep up the pressure.
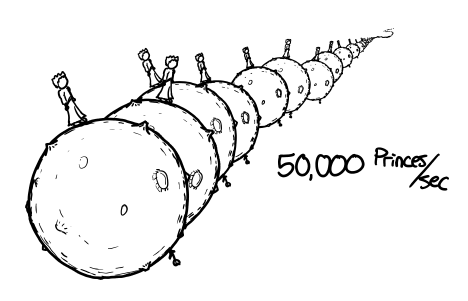
Unfortunately, the steady high-altitude meteor shower would deliver just as much energy to the atmosphere that daily giant impacts would, and the eventual death toll would be the same: Seven billion humans, plus four billion Little Princes per day.
But at least we could stop worrying about leap seconds.